
Question Number 222848 by MrGaster last updated on 09/Jul/25
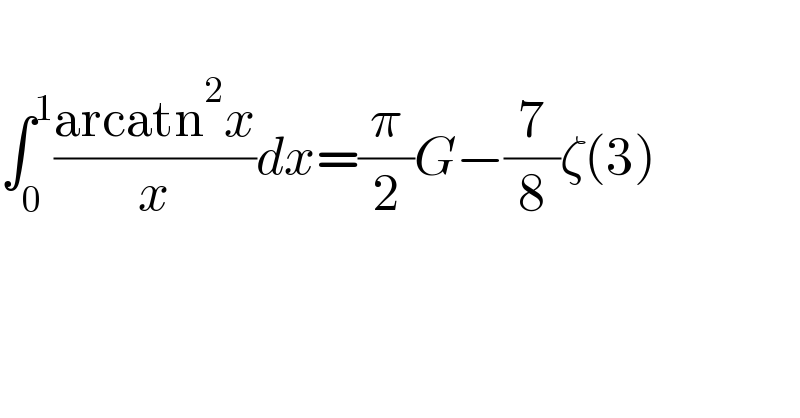
$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{arcatn}^{\mathrm{2}} {x}}{{x}}{dx}=\frac{\pi}{\mathrm{2}}{G}−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$
Answered by MrGaster last updated on 09/Jul/25
![cos x=Σ_(n=0) ^∞ sin(2n+1)x I=∫_0 ^(arctan) (x^2 /(tan x))=∫_0 ^(π/4) (x^2 /(tanx))sec^2 xdx=∫_0 ^(π/4) (x^2 /(sinxcosx))dx =2∫_0 ^(π/4) (x^2 /(sinx))dx=2∫_0 ^(π/4) (((x/2)^2 )/(sinx))dx/2=(1/4)∫_0 ^(π/2) (x^2 /(sinx))dx,G=0.915965594177219 =(1/4)∫_0 ^(π/2) x^2 2Σ_(n=0) ^∞ sin(2n+1)xdx=(1/2)Σ_(n=0) ^∞ ∫_0 ^(π/2) x^2 sin(2n+1)xdx =(1/2)Σ_(n=0) ^∞ [((π(−1)^n )/((2n−1)^2 ))−(2/((2n+1)^3 ))]=(π/2)Σ_(n=0) ^∞ (((−1)^n )/((2n−1)^2 ))−Σ_(n=0) ^∞ (1/((2n+1)^3 )) =(π/2)G−(7/8)ζ(3)](Q222849.png)
$$\mathrm{cos}\:{x}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{sin}\left(\mathrm{2}{n}+\mathrm{1}\right){x} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{arctan}} \frac{{x}^{\mathrm{2}} }{\mathrm{tan}\:{x}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{x}^{\mathrm{2}} }{\mathrm{tan}{x}}\mathrm{sec}^{\mathrm{2}} {xdx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{x}^{\mathrm{2}} }{\mathrm{sin}{x}\mathrm{cos}{x}}{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{x}^{\mathrm{2}} }{\mathrm{sin}{x}}{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left({x}/\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{sin}{x}}{dx}/\mathrm{2}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}^{\mathrm{2}} }{\mathrm{sin}{x}}{dx},{G}=\mathrm{0}.\mathrm{915965594177219} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} \mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{sin}\left(\mathrm{2}{n}+\mathrm{1}\right){xdx}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{2}{n}+\mathrm{1}\right){xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\pi\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\right]=\frac{\pi}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\pi}{\mathrm{2}}{G}−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$
