Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 171665 by Mastermind last updated on 19/Jun/22

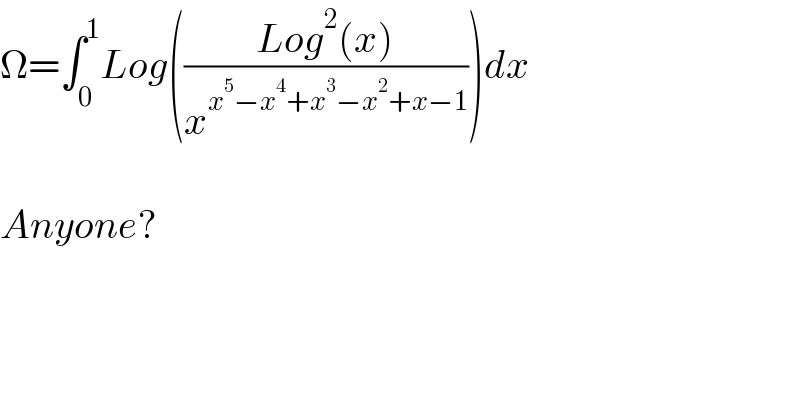
Ω=∫_0 ^1 Log(((Log^2 (x))/x^(x^5 −x^4 +x^3 −x^2 +x−1) ))dx Anyone?

$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} {Log}\left(\frac{{Log}^{\mathrm{2}} \left({x}\right)}{{x}^{{x}^{\mathrm{5}} −{x}^{\mathrm{4}} +{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}−\mathrm{1}} }\right){dx} \\ $$$$ \\ $$$${Anyone}? \\ $$

Answered by mindispower last updated on 19/Jun/22

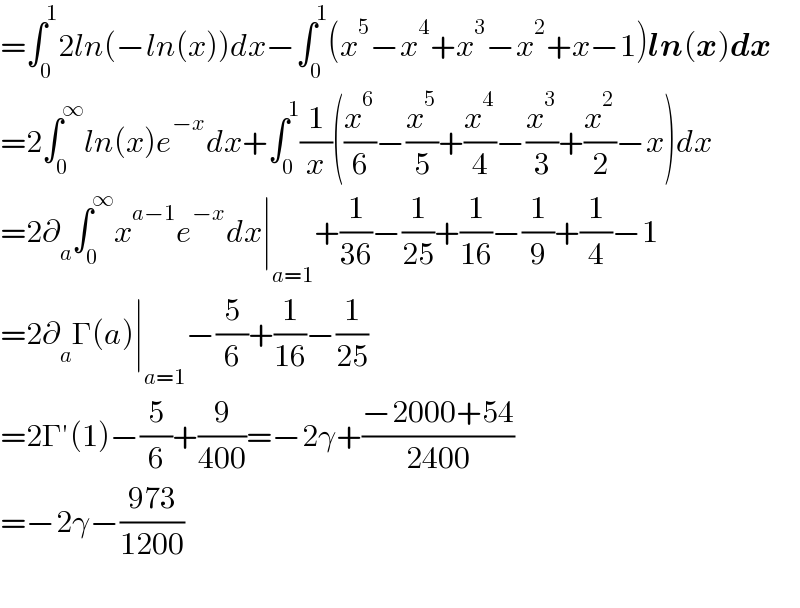
=∫_0 ^1 2ln(−ln(x))dx−∫_0 ^1 (x^5 −x^4 +x^3 −x^2 +x−1)ln(x)dx =2∫_0 ^∞ ln(x)e^(−x) dx+∫_0 ^1 (1/x)((x^6 /6)−(x^5 /5)+(x^4 /4)−(x^3 /3)+(x^2 /2)−x)dx =2∂_a ∫_0 ^∞ x^(a−1) e^(−x) dx∣_(a=1) +(1/(36))−(1/(25))+(1/(16))−(1/9)+(1/4)−1 =2∂_a Γ(a)∣_(a=1) −(5/6)+(1/(16))−(1/(25)) =2Γ′(1)−(5/6)+(9/(400))=−2γ+((−2000+54)/(2400)) =−2γ−((973)/(1200))

$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{ln}\left(−{ln}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{5}} −{x}^{\mathrm{4}} +{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +{x}−\mathrm{1}\right)\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} {ln}\left({x}\right){e}^{−{x}} {dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\left(\frac{{x}^{\mathrm{6}} }{\mathrm{6}}−\frac{{x}^{\mathrm{5}} }{\mathrm{5}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}\right){dx} \\ $$$$=\mathrm{2}\partial_{{a}} \int_{\mathrm{0}} ^{\infty} {x}^{{a}−\mathrm{1}} {e}^{−{x}} {dx}\mid_{{a}=\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{36}}−\frac{\mathrm{1}}{\mathrm{25}}+\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1} \\ $$$$=\mathrm{2}\partial_{{a}} \Gamma\left({a}\right)\mid_{{a}=\mathrm{1}} −\frac{\mathrm{5}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$=\mathrm{2}\Gamma'\left(\mathrm{1}\right)−\frac{\mathrm{5}}{\mathrm{6}}+\frac{\mathrm{9}}{\mathrm{400}}=−\mathrm{2}\gamma+\frac{−\mathrm{2000}+\mathrm{54}}{\mathrm{2400}} \\ $$$$=−\mathrm{2}\gamma−\frac{\mathrm{973}}{\mathrm{1200}} \\ $$$$ \\ $$

Commented by Mastermind last updated on 19/Jun/22

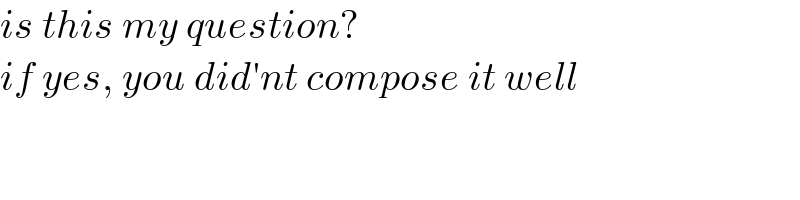
is this my question? if yes, you did′nt compose it well

$${is}\:{this}\:{my}\:{question}? \\ $$$${if}\:{yes},\:{you}\:{did}'{nt}\:{compose}\:{it}\:{well} \\ $$

Commented by mindispower last updated on 19/Jun/22

ln(−ln(x)) value of integral is coorect

$${ln}\left(−{ln}\left({x}\right)\right)\:{value}\:{of}\:{integral}\:{is}\:{coorect} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com