
Question Number 119659 by ZiYangLee last updated on 26/Oct/20
![∫_0 ^1 [(4x−1)f(12x^2 −6x)]dx=?](Q119659.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left[\left(\mathrm{4}{x}−\mathrm{1}\right){f}\left(\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}{x}\right)\right]{dx}=? \\ $$
Answered by bemath last updated on 26/Oct/20
![let u = 12x^2 −6x →du = 24x−6 dx (1/6)du = (4x−1) dx with { ((x=0→u=0)),((x=1→u=6)) :} ∫_0 ^6 (1/6)f(u) du = (1/6)[ F(u) ]_0 ^6 = (1/6) [ F(6)−F(0) ] where F(u) anti derivative of function f(u)](Q119666.png)
$${let}\:{u}\:=\:\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}{x}\:\rightarrow{du}\:=\:\mathrm{24}{x}−\mathrm{6}\:{dx} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{6}}{du}\:=\:\left(\mathrm{4}{x}−\mathrm{1}\right)\:{dx}\: \\ $$$$\:{with}\:\begin{cases}{{x}=\mathrm{0}\rightarrow{u}=\mathrm{0}}\\{{x}=\mathrm{1}\rightarrow{u}=\mathrm{6}}\end{cases} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{6}} {\int}}\:\frac{\mathrm{1}}{\mathrm{6}}{f}\left({u}\right)\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left[\:{F}\left({u}\right)\:\right]_{\mathrm{0}} ^{\mathrm{6}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{6}}\:\left[\:{F}\left(\mathrm{6}\right)−{F}\left(\mathrm{0}\right)\:\right]\: \\ $$$${where}\:{F}\left({u}\right)\:{anti}\:{derivative}\:{of}\:{function}\:{f}\left({u}\right) \\ $$
Commented by ZiYangLee last updated on 26/Oct/20

$$\mathrm{thanks} \\ $$
Answered by mathmax by abdo last updated on 26/Oct/20
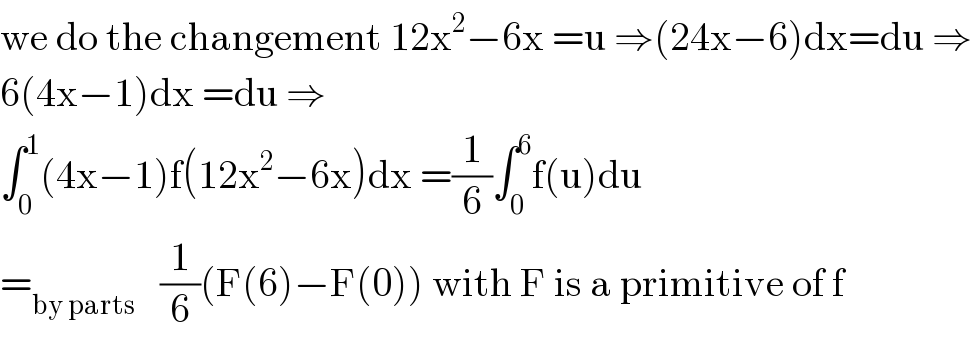
$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{12x}^{\mathrm{2}} −\mathrm{6x}\:=\mathrm{u}\:\Rightarrow\left(\mathrm{24x}−\mathrm{6}\right)\mathrm{dx}=\mathrm{du}\:\Rightarrow \\ $$$$\mathrm{6}\left(\mathrm{4x}−\mathrm{1}\right)\mathrm{dx}\:=\mathrm{du}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{4x}−\mathrm{1}\right)\mathrm{f}\left(\mathrm{12x}^{\mathrm{2}} −\mathrm{6x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{6}} \mathrm{f}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{F}\left(\mathrm{6}\right)−\mathrm{F}\left(\mathrm{0}\right)\right)\:\mathrm{with}\:\mathrm{F}\:\mathrm{is}\:\mathrm{a}\:\mathrm{primitive}\:\mathrm{of}\:\mathrm{f} \\ $$
