
Question Number 131147 by EDWIN88 last updated on 02/Feb/21
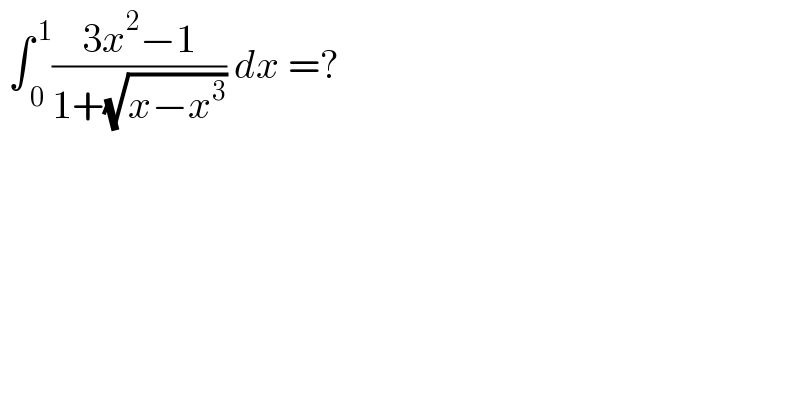
$$\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\sqrt{{x}−{x}^{\mathrm{3}} }}\:{dx}\:=?\: \\ $$
Commented by EDWIN88 last updated on 02/Feb/21
![(√(x−x^3 )) = w−1 ⇒x−x^3 =(w−1)^2 (1−3x^2 )dx=2(w−1)dw I=−∫_1 ^1 ((2w−1)/w) dw = ∫_1 ^( 1) ((1/w)−2)dw = [ ln ∣w∣−2w ]_1 ^1 = −2 −(−2) = 0](Q131154.png)
$$\:\sqrt{{x}−{x}^{\mathrm{3}} }\:=\:{w}−\mathrm{1}\:\Rightarrow{x}−{x}^{\mathrm{3}} =\left({w}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\left(\mathrm{1}−\mathrm{3}{x}^{\mathrm{2}} \right){dx}=\mathrm{2}\left({w}−\mathrm{1}\right){dw}\: \\ $$$${I}=−\int_{\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{2}{w}−\mathrm{1}}{{w}}\:{dw}\:=\:\int_{\mathrm{1}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{{w}}−\mathrm{2}\right){dw} \\ $$$$=\:\left[\:\mathrm{ln}\:\mid{w}\mid−\mathrm{2}{w}\:\right]_{\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\:−\mathrm{2}\:−\left(−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 02/Feb/21
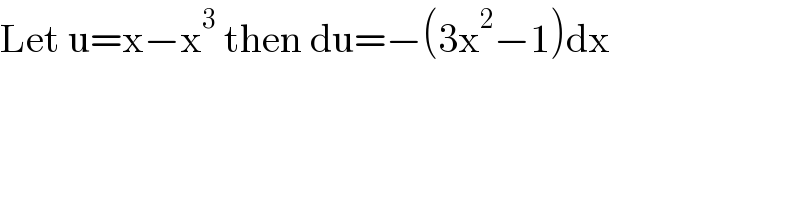
$$\mathrm{Let}\:\mathrm{u}=\mathrm{x}−\mathrm{x}^{\mathrm{3}} \:\mathrm{then}\:\mathrm{du}=−\left(\mathrm{3x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{dx} \\ $$
