Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 220889 by Nicholas666 last updated on 20/May/25

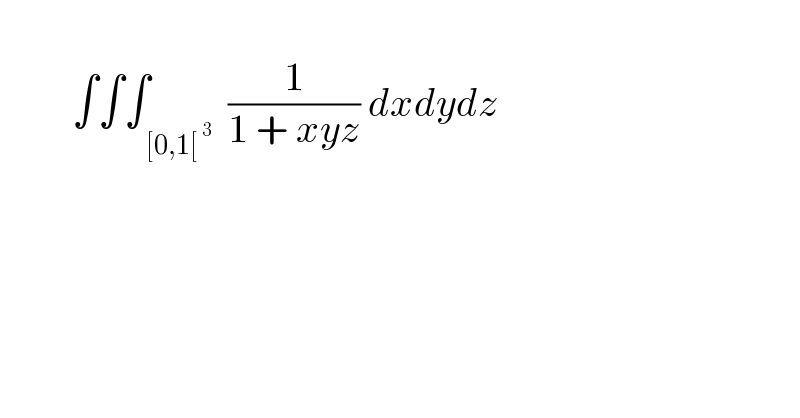
∫∫∫_( [0,1[^( 3) ) (1/(1 + xyz)) dxdydz

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\int\int\int_{\:\left[\mathrm{0},\mathrm{1}\left[^{\:\mathrm{3}} \right.\right.} \:\frac{\mathrm{1}}{\mathrm{1}\:+\:{xyz}}\:{dxdydz} \\ $$$$ \\ $$

Answered by breniam last updated on 20/May/25

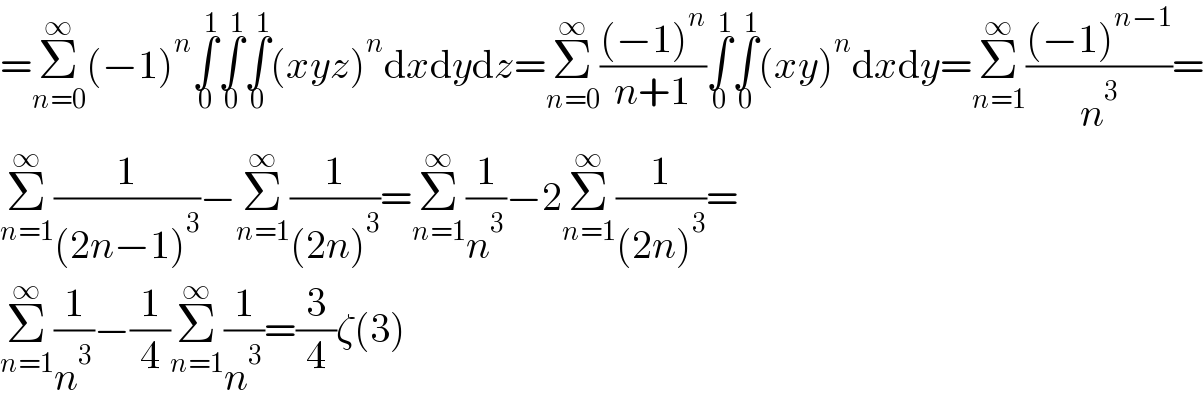
=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 ∫_0 ^1 ∫_0 ^1 (xyz)^n dxdydz=Σ_(n=0) ^∞ (((−1)^n )/(n+1))∫_0 ^1 ∫_0 ^1 (xy)^n dxdy=Σ_(n=1) ^∞ (((−1)^(n−1) )/n^3 )= Σ_(n=1) ^∞ (1/((2n−1)^3 ))−Σ_(n=1) ^∞ (1/((2n)^3 ))=Σ_(n=1) ^∞ (1/n^3 )−2Σ_(n=1) ^∞ (1/((2n)^3 ))= Σ_(n=1) ^∞ (1/n^3 )−(1/4)Σ_(n=1) ^∞ (1/n^3 )=(3/4)ζ(3)

$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({xyz}\right)^{{n}} \mathrm{d}{x}\mathrm{d}{y}\mathrm{d}{z}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({xy}\right)^{{n}} \mathrm{d}{x}\mathrm{d}{y}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{3}} }= \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{3}} }−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{3}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{3}} }= \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} }=\frac{\mathrm{3}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$

Answered by Wuji last updated on 20/May/25

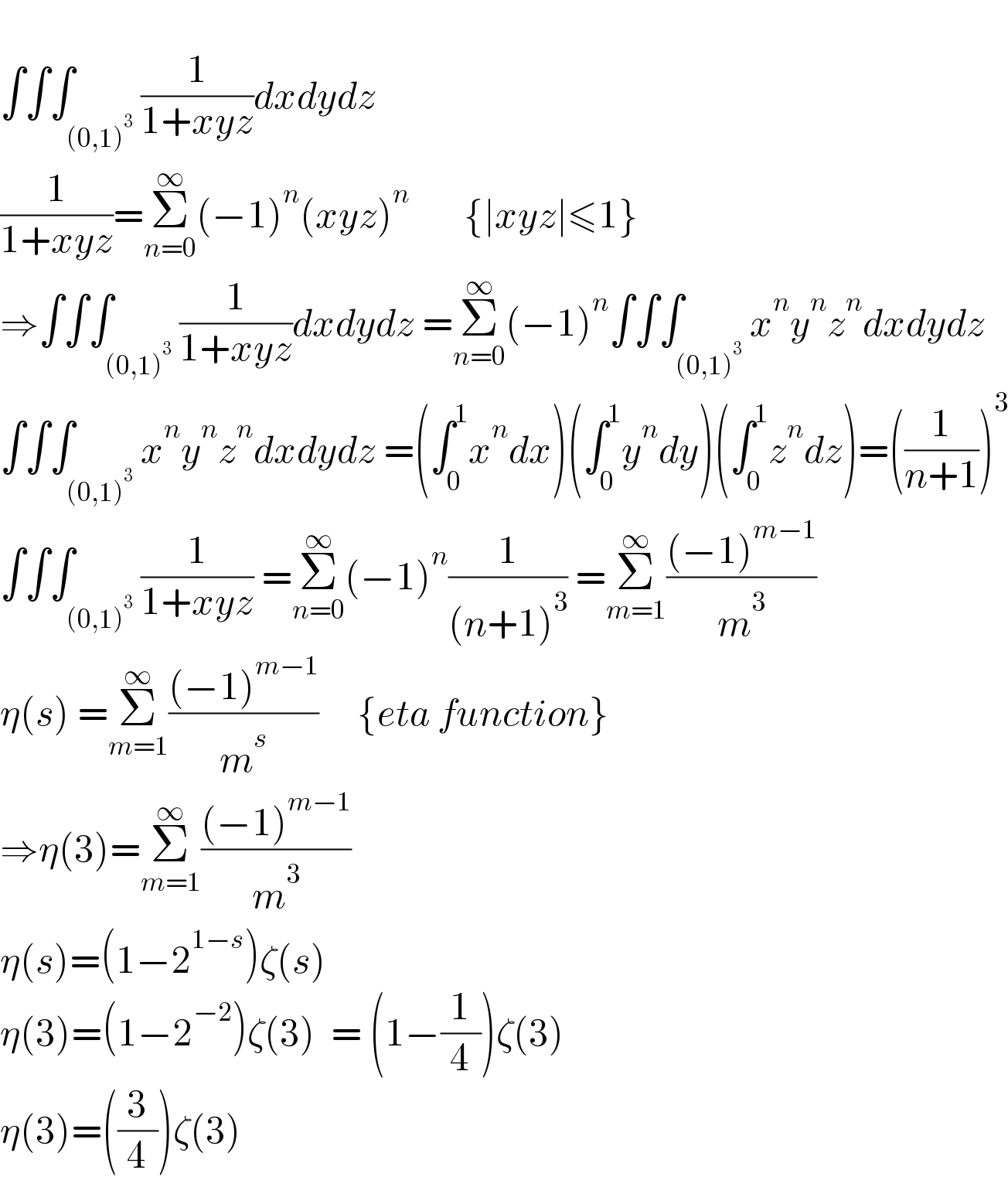
∫∫∫_((0,1)^3 ) (1/(1+xyz))dxdydz (1/(1+xyz))=Σ_(n=0) ^∞ (−1)^n (xyz)^n {∣xyz∣≤1} ⇒∫∫∫_((0,1)^3 ) (1/(1+xyz))dxdydz =Σ_(n=0) ^∞ (−1)^n ∫∫∫_((0,1)^3 ) x^n y^n z^n dxdydz ∫∫∫_((0,1)^3 ) x^n y^n z^n dxdydz =(∫_0 ^1 x^n dx)(∫_0 ^1 y^n dy)(∫_0 ^1 z^n dz)=((1/(n+1)))^3 ∫∫∫_((0,1)^3 ) (1/(1+xyz)) =Σ_(n=0) ^∞ (−1)^n (1/((n+1)^3 )) =Σ_(m=1) ^∞ (((−1)^(m−1) )/m^3 ) η(s) =Σ_(m=1) ^∞ (((−1)^(m−1) )/m^s ) {eta function} ⇒η(3)=Σ_(m=1) ^∞ (((−1)^(m−1) )/m^3 ) η(s)=(1−2^(1−s) )ζ(s) η(3)=(1−2^(−2) )ζ(3) = (1−(1/4))ζ(3) η(3)=((3/4))ζ(3)

$$ \\ $$$$\int\int\int_{\left(\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } \frac{\mathrm{1}}{\mathrm{1}+{xyz}}{dxdydz} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{xyz}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left({xyz}\right)^{{n}} \:\:\:\:\:\:\:\left\{\mid{xyz}\mid\leqslant\mathrm{1}\right\} \\ $$$$\Rightarrow\int\int\int_{\left(\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } \frac{\mathrm{1}}{\mathrm{1}+{xyz}}{dxdydz}\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int\int\int_{\left(\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } {x}^{{n}} {y}^{{n}} {z}^{{n}} {dxdydz} \\ $$$$\int\int\int_{\left(\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } {x}^{{n}} {y}^{{n}} {z}^{{n}} {dxdydz}\:=\left(\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {dx}\right)\left(\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{n}} {dy}\right)\left(\int_{\mathrm{0}} ^{\mathrm{1}} {z}^{{n}} {dz}\right)=\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)^{\mathrm{3}} \\ $$$$\int\int\int_{\left(\mathrm{0},\mathrm{1}\right)^{\mathrm{3}} } \frac{\mathrm{1}}{\mathrm{1}+{xyz}}\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\:=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−\mathrm{1}} }{{m}^{\mathrm{3}} } \\ $$$$\eta\left({s}\right)\:=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−\mathrm{1}} }{{m}^{{s}} }\:\:\:\:\:\left\{{eta}\:{function}\right\} \\ $$$$\Rightarrow\eta\left(\mathrm{3}\right)=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−\mathrm{1}} }{{m}^{\mathrm{3}} }\: \\ $$$$\eta\left({s}\right)=\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right)\zeta\left({s}\right) \\ $$$$\eta\left(\mathrm{3}\right)=\left(\mathrm{1}−\mathrm{2}^{−\mathrm{2}} \right)\zeta\left(\mathrm{3}\right)\:\:=\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)\zeta\left(\mathrm{3}\right) \\ $$$$\eta\left(\mathrm{3}\right)=\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\zeta\left(\mathrm{3}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com