
Question Number 222996 by MrGaster last updated on 12/Jul/25
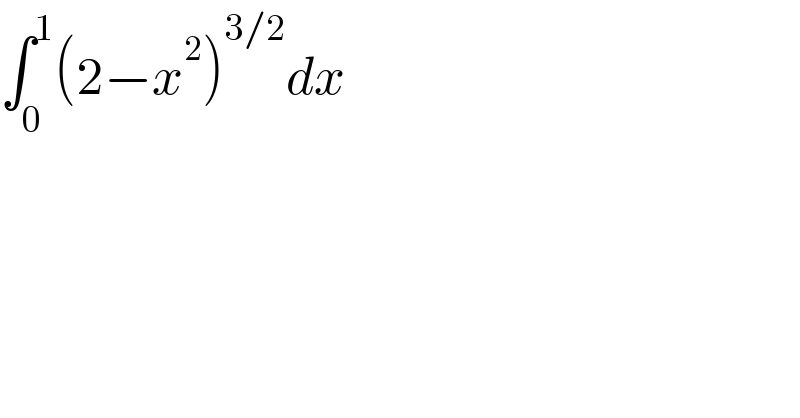
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} {dx} \\ $$
Answered by MrGaster last updated on 12/Jul/25
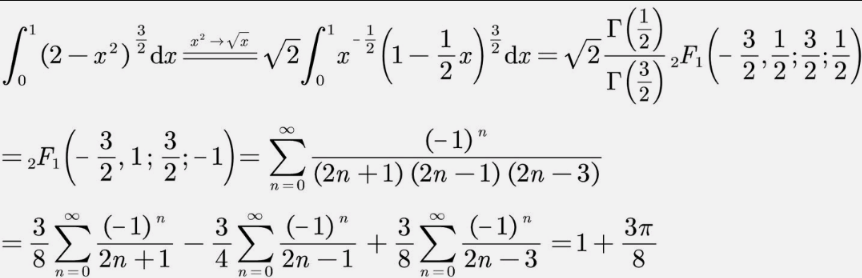
Answered by MrGaster last updated on 12/Jul/25
![(2):x=(√2)sinθ,dx=(√2)cosθdθ,θ∈[0,(π/4)] =∫_0 ^(π/4) (2−2sin^2 θ)^(3/2) (√2)cosθdθ=∫_0 ^(π/4) [2cos^2 θ]^(3/2) (√2)cosθdθ=∫_0 ^(π/4) 2^(3/2) cos^3 θ∙(√2)cosθdθ =∫_0 ^(π/4) 2^2 cos^4 θdθ=4∫_0 ^(π/4) cos^4 θdθ cos^4 θ(((1+cos2θ)/θ))^2 =(1/4)(1+2cos2θ+cos^2 2θ)=(1/4)(1+2 cos 2θ+((1−cos4θ)/2)) =(1/4)((3/2)+2cos2θ+(1/2)cos4θ)=(3/8)+(1/2)cos2θ+(1/8)cos4θ ∫_0 ^(π/4) cos^4 θdθ=∫_0 ^(π/4) ((3/8)+(1/2)cos2θ+(1/8)cos 4θ)dθ=[(3/8)θ+(1/4)sin2θ+(1/(32))sin4θ]_0 ^(π/4) =((3/8)∙(π/4)+(1/4)sin(π/2)+(1/(32))sin π)−(0+0+0)=((3π)/(32))+(1/4)∙1+0=((3π)/(32))+(1/4) 4×(((3π)/(32))+(1/4))=4∙((3π)/(32))+4∙(1/4)=((12π)/(32))+1=((3π)/8)+1](Q222998.png)
$$\left(\mathrm{2}\right):{x}=\sqrt{\mathrm{2}}\mathrm{sin}\theta,{dx}=\sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta,\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right] \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \left(\mathrm{2}−\mathrm{2sin}^{\mathrm{2}} \theta\right)^{\mathrm{3}/\mathrm{2}} \sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \left[\mathrm{2cos}^{\mathrm{2}} \theta\right]^{\mathrm{3}/\mathrm{2}} \sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{2}^{\mathrm{3}/\mathrm{2}} \mathrm{cos}^{\mathrm{3}} \theta\centerdot\sqrt{\mathrm{2}}\mathrm{cos}\theta\mathrm{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{2}^{\mathrm{2}} \mathrm{cos}^{\mathrm{4}} \theta\mathrm{d}\theta=\mathrm{4}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{cos}^{\mathrm{4}} \theta\mathrm{d}\theta \\ $$$$\mathrm{cos}^{\mathrm{4}} \theta\left(\frac{\mathrm{1}+\mathrm{cos2}\theta}{\theta}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2cos2}\theta+\mathrm{cos}^{\mathrm{2}} \mathrm{2}\theta\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\theta+\frac{\mathrm{1}−\mathrm{cos4}\theta}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2cos2}\theta+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos4}\theta\right)=\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos4}\theta \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \mathrm{cos}^{\mathrm{4}} \theta\mathrm{d}\theta=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2}\theta+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{cos}\:\mathrm{4}\theta\right)\mathrm{d}\theta=\left[\frac{\mathrm{3}}{\mathrm{8}}\theta+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin2}\theta+\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin4}\theta\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$=\left(\frac{\mathrm{3}}{\mathrm{8}}\centerdot\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{32}}\mathrm{sin}\:\pi\right)−\left(\mathrm{0}+\mathrm{0}+\mathrm{0}\right)=\frac{\mathrm{3}\pi}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{4}}\centerdot\mathrm{1}+\mathrm{0}=\frac{\mathrm{3}\pi}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{4}×\left(\frac{\mathrm{3}\pi}{\mathrm{32}}+\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{4}\centerdot\frac{\mathrm{3}\pi}{\mathrm{32}}+\mathrm{4}\centerdot\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{12}\pi}{\mathrm{32}}+\mathrm{1}=\frac{\mathrm{3}\pi}{\mathrm{8}}+\mathrm{1} \\ $$
