
Question Number 86613 by Ar Brandon last updated on 29/Mar/20
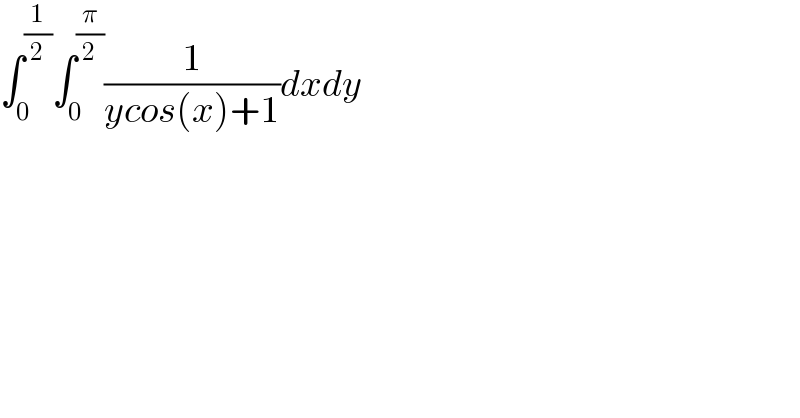
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{ycos}\left({x}\right)+\mathrm{1}}{dxdy} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 29/Mar/20

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{{y}\:{cosx}+\mathrm{1}}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({y}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{y}−{yt}^{\mathrm{2}} \:+\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dy}}{\left(\mathrm{1}−{y}\right){t}^{\mathrm{2}} +\mathrm{1}+{y}} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}−{y}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dy}}{{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}} \\ $$$$=_{{t}\:=\sqrt{\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}}{u}} \:\:\:\:\frac{\mathrm{2}}{\left(\mathrm{1}−{y}\right)}×\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}\:\:\int_{\mathrm{0}} ^{\sqrt{\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }×\sqrt{\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}}{du} \\ $$$$=\:\frac{\mathrm{2}}{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}\:{arctan}\left(\sqrt{\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dxdy}}{{ycosx}\:+\mathrm{1}}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}\:{arctan}\left(\sqrt{\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}}\right){dy} \\ $$$$...{be}\:{continued}... \\ $$
Commented by mind is power last updated on 30/Mar/20
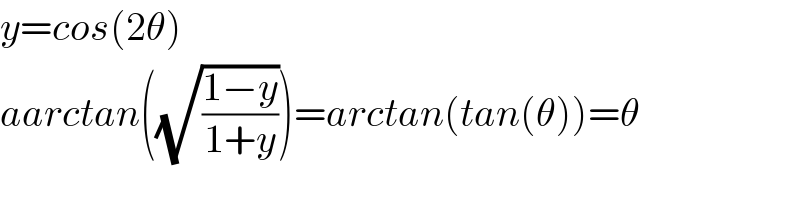
$${y}={cos}\left(\mathrm{2}\theta\right) \\ $$$${aarctan}\left(\sqrt{\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}}\right)={arctan}\left({tan}\left(\theta\right)\right)=\theta \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
![changement y=cosθ give ∫_0 ^(1/2) (1/(√(1−y^2 )))arctan((√((1−y)/(1+y))))dy =∫_(π/2) ^(π/3) (1/(sinθ)) arctan((√((2sin^2 ((θ/2)))/(2cos^2 ((θ/2))))))(−sinθ)dθ = ∫_(π/3) ^(π/2) arctan(tan((θ/2))) dθ =(1/2) ∫_(π/3) ^(π/2) θ dθ =(1/2)[(θ^2 /2)]_(π/3) ^(π/2) =(1/4)( (π^2 /4)−(π^2 /9)) =(1/4)(((9π^2 −4π^2 )/(36))) =((5π^2 )/(144))](Q86718.png)
$${changement}\:{y}={cos}\theta\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }}{arctan}\left(\sqrt{\frac{\mathrm{1}−{y}}{\mathrm{1}+{y}}}\right){dy}\:=\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{1}}{{sin}\theta}\:{arctan}\left(\sqrt{\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)}}\right)\left(−{sin}\theta\right){d}\theta \\ $$$$=\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:{arctan}\left({tan}\left(\frac{\theta}{\mathrm{2}}\right)\right)\:{d}\theta\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \theta\:{d}\theta\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\theta^{\mathrm{2}} }{\mathrm{2}}\right]_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\:\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\frac{\pi^{\mathrm{2}} }{\mathrm{9}}\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{9}\pi^{\mathrm{2}} −\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{36}}\right)\:=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{144}} \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
$${thank}\:{you}\:{sir}\:{mind}.. \\ $$
Commented by Ar Brandon last updated on 30/Mar/20

$${great}\:\:{job} \\ $$
Commented by abdomathmax last updated on 30/Mar/20
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
