
Question Number 122069 by Dwaipayan Shikari last updated on 13/Nov/20
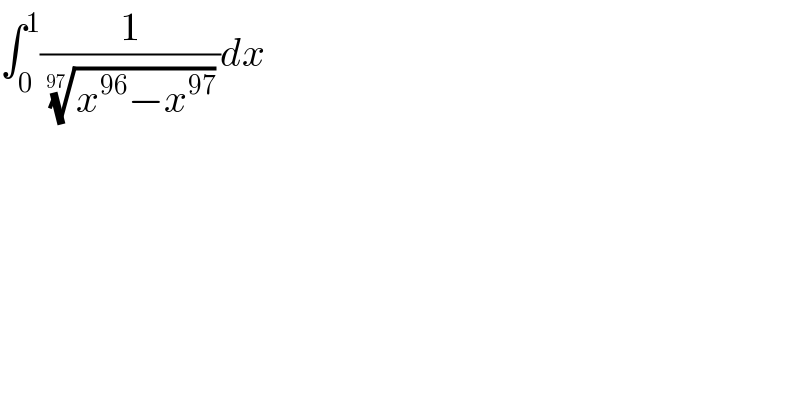
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{\mathrm{97}}]{{x}^{\mathrm{96}} −{x}^{\mathrm{97}} }}{dx} \\ $$
Answered by mindispower last updated on 14/Nov/20
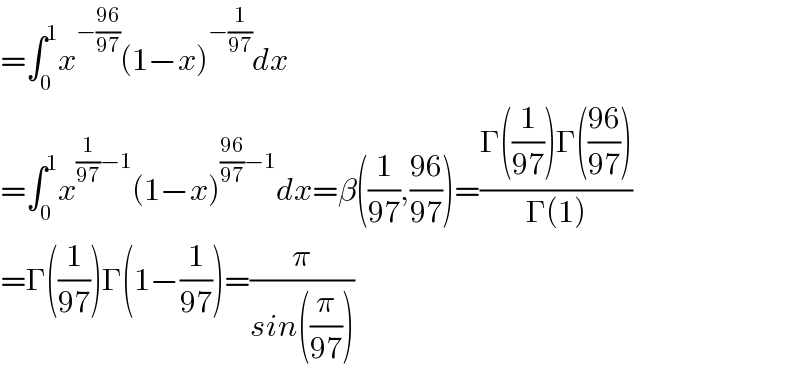
$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{96}}{\mathrm{97}}} \left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{97}}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\frac{\mathrm{1}}{\mathrm{97}}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{96}}{\mathrm{97}}−\mathrm{1}} {dx}=\beta\left(\frac{\mathrm{1}}{\mathrm{97}},\frac{\mathrm{96}}{\mathrm{97}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{97}}\right)\Gamma\left(\frac{\mathrm{96}}{\mathrm{97}}\right)}{\Gamma\left(\mathrm{1}\right)} \\ $$$$=\Gamma\left(\frac{\mathrm{1}}{\mathrm{97}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{97}}\right)=\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{97}}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 14/Nov/20
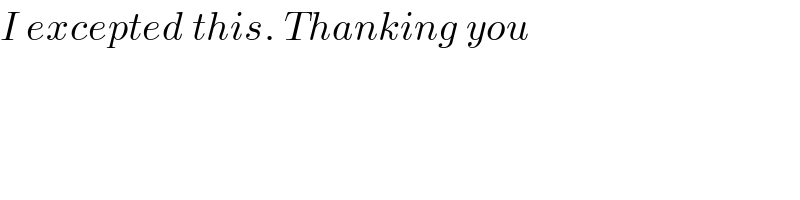
$${I}\:{excepted}\:{this}.\:{Thanking}\:{you} \\ $$
Commented by mindispower last updated on 14/Nov/20

$${withe}\:{pleaser}\:{sir}\:,{i}\:{find}\:{the}\:{previous}\:{sum} \\ $$$${you}\:{right}\:\mathrm{1}/\mathrm{24}\:{nice}\:{day}\:{god}\:{bless}\:{you} \\ $$
