
Question Number 53078 by gunawan last updated on 16/Jan/19
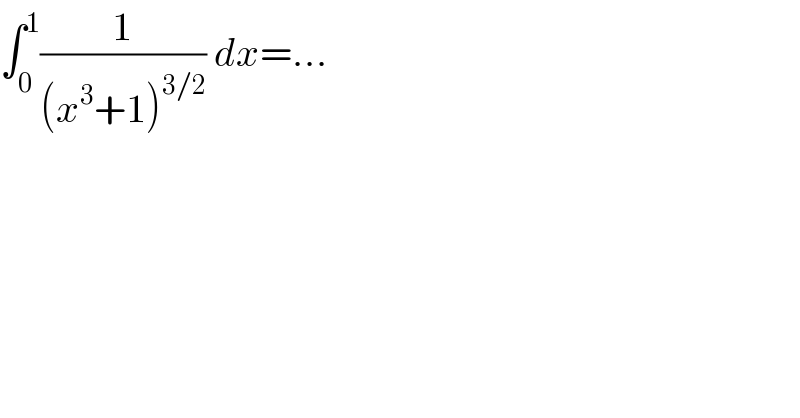
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }\:{dx}=... \\ $$
Commented by MJS last updated on 17/Jan/19

$$\approx.\mathrm{774606} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
![1+x^3 >1+x^2 (1/(1+x^3 ))<(1/(1+x^2 )) but in the interval [0,1] (1/((1+x^3 )^(3/2) ))>(1/((1+x^2 )^(3/2) so)) i am rectifying ∫_0 ^1 (dx/((1+x^3 )^(3/2) ))>∫_0 ^1 (dx/((1+x^2 )^(3/2) )) now ∫_0 ^1 (dx/((1+x^2 )^(3/2) )) x=tana ∫_0 ^(π/4) ((sec^2 a)/((1+tan^2 a)^(3/2) ))da ∫_0 ^(π/4) ((sec^2 ada)/(sec^3 a)) ∫_0 ^(π/4) cosada ∣sina∣_0 ^(π/4) =(1/(√2)) so I>(1/(√2)) I>0.71 attaching graph... answer yet to find....](Q53088.png)
$$\mathrm{1}+{x}^{\mathrm{3}} >\mathrm{1}+{x}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }<\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${but}\:{in}\:{the}\:{interval}\:\left[\mathrm{0},\mathrm{1}\right] \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }>\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} {so}} \\ $$$${i}\:{am}\:{rectifying} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }>\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${now}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${x}={tana}\:\:\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} {a}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{da} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{sec}^{\mathrm{2}} {ada}}{{sec}^{\mathrm{3}} {a}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cosada} \\ $$$$\mid{sina}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$${so}\:\:\:\:\:\:{I}>\frac{\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$$${I}>\mathrm{0}.\mathrm{71} \\ $$$${attaching}\:{graph}... \\ $$$${answer}\:{yet}\:{to}\:{find}.... \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jan/19
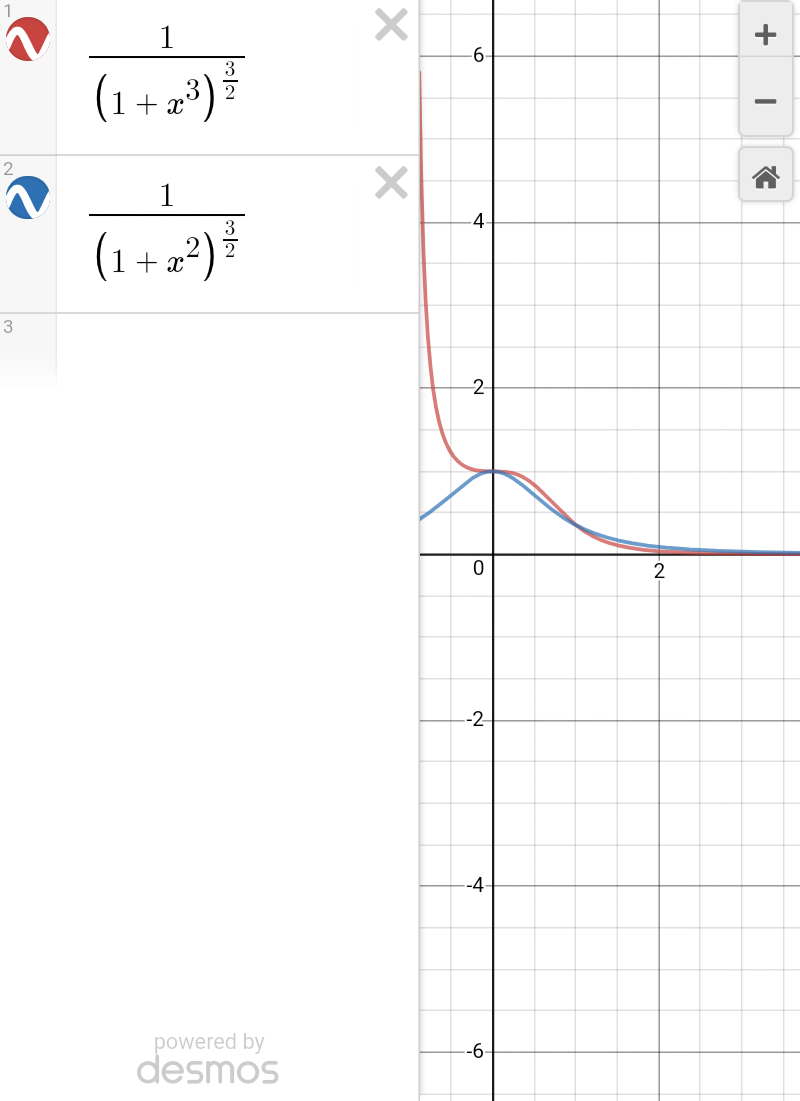
![area of trapazium calculation whenf(x)=(1/((1+x^3 )^(3/2) )) at x=1 f(1)=(1/((2)^(3/2) ))=(1/(2(√2))) at x=0 f(0)=(1/((1+0)^(3/2) ))=1 so area of trapazium=(1/2)[f(0)+f(1)]×1 =(1/2)(1+(1/(2(√2))))×1=0.68 from graph it is clear that area bounded i,e ∫_0 ^1 (dx/((1+x^3 )^(3/2) ))>0.68](Q53092.png)
$${area}\:{of}\:{trapazium}\:{calculation} \\ $$$${whenf}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${at}\:{x}=\mathrm{1}\:\:\:{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\left(\mathrm{2}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${at}\:{x}=\mathrm{0}\:\:{f}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{0}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\mathrm{1} \\ $$$${so}\:{area}\:{of}\:{trapazium}=\frac{\mathrm{1}}{\mathrm{2}}\left[{f}\left(\mathrm{0}\right)+{f}\left(\mathrm{1}\right)\right]×\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)×\mathrm{1}=\mathrm{0}.\mathrm{68} \\ $$$${from}\:{graph}\:{it}\:{is}\:{clear}\:{that}\:{area}\:{bounded}\:{i},{e} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }>\mathrm{0}.\mathrm{68} \\ $$$$ \\ $$
