
Question Number 83226 by 09658867628 last updated on 28/Feb/20
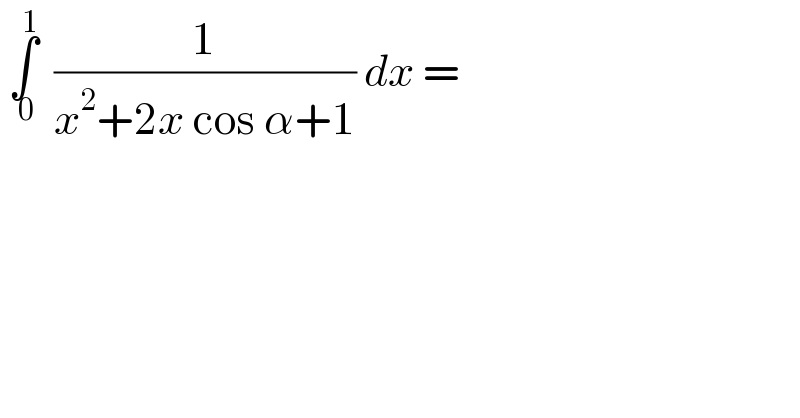
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}{x}\:\mathrm{cos}\:\alpha+\mathrm{1}}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 29/Feb/20
![I =∫_0 ^1 (dx/((x+cosα)^2 +sin^2 α))changement x+cosα =sinα)u give I =∫_(cotanα) ^((1+cosα)/(sinα)) ((sinα du)/(sin^2 α(1+u^2 ))) =(1/(sinα))[arctanu]_(1/(tanα)) ^(1/(tan((α/2)))) =(1/(sinα)){ arctan((1/(tan((α/2)))))−arctan((1/(tanα)))} if tanα>0 we get I =(1/(sinα)){(π/2)−(α/2)−(π/2) +α} =(α/(2sinα)) ....](Q83249.png)
$$\left.{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left({x}+{cos}\alpha\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \alpha}{changement}\:{x}+{cos}\alpha\:={sin}\alpha\right){u}\:{give} \\ $$$${I}\:=\int_{{cotan}\alpha} ^{\frac{\mathrm{1}+{cos}\alpha}{{sin}\alpha}} \:\:\frac{{sin}\alpha\:{du}}{{sin}^{\mathrm{2}} \alpha\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{sin}\alpha}\left[{arctanu}\right]_{\frac{\mathrm{1}}{{tan}\alpha}} ^{\frac{\mathrm{1}}{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)}} \\ $$$$=\frac{\mathrm{1}}{{sin}\alpha}\left\{\:{arctan}\left(\frac{\mathrm{1}}{{tan}\left(\frac{\alpha}{\mathrm{2}}\right)}\right)−{arctan}\left(\frac{\mathrm{1}}{{tan}\alpha}\right)\right\} \\ $$$${if}\:{tan}\alpha>\mathrm{0}\:{we}\:{get}\:{I}\:=\frac{\mathrm{1}}{{sin}\alpha}\left\{\frac{\pi}{\mathrm{2}}−\frac{\alpha}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\:+\alpha\right\}\:=\frac{\alpha}{\mathrm{2}{sin}\alpha}\:.... \\ $$
Answered by MJS last updated on 28/Feb/20
![∫(dx/(x^2 +2xcos α +1))= =∫(dx/((x+cos α)^2 +1−cos^2 α))= [t=((x+cos α)/(√(1−cos^2 α))) → dx=dt(√(1−cos^2 α))] [of course (√(1−cos^2 α))=∣sin α∣] =(1/(∣sin α∣))∫(dt/(t^2 +1))=((arctan t)/(∣sin α∣))=((arctan ((x+cos α)/(∣sin α∣)))/(∣sin α∣)) +C](Q83236.png)
$$\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{cos}\:\alpha\:+\mathrm{1}}= \\ $$$$=\int\frac{{dx}}{\left({x}+\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}+\mathrm{cos}\:\alpha}{\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}}\:\rightarrow\:{dx}={dt}\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}\right] \\ $$$$\:\:\:\:\:\left[\mathrm{of}\:\mathrm{course}\:\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\alpha}=\mid\mathrm{sin}\:\alpha\mid\right] \\ $$$$=\frac{\mathrm{1}}{\mid\mathrm{sin}\:\alpha\mid}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{arctan}\:{t}}{\mid\mathrm{sin}\:\alpha\mid}=\frac{\mathrm{arctan}\:\frac{{x}+\mathrm{cos}\:\alpha}{\mid\mathrm{sin}\:\alpha\mid}}{\mid\mathrm{sin}\:\alpha\mid}\:+{C} \\ $$
