
Question Number 144876 by qaz last updated on 30/Jun/21
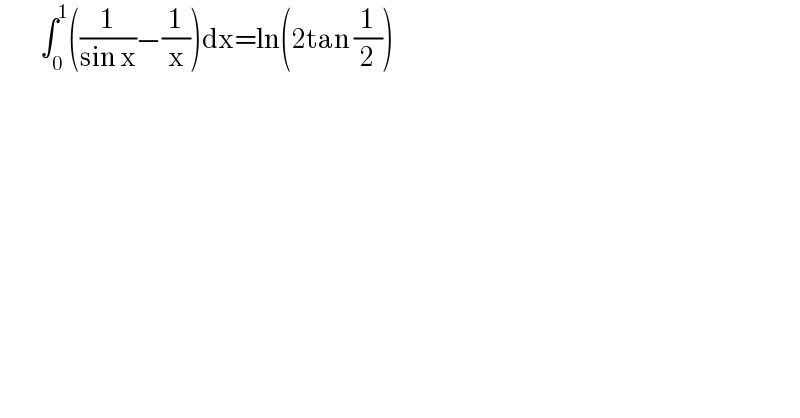
$$\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx}=\mathrm{ln}\left(\mathrm{2tan}\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Answered by mindispower last updated on 30/Jun/21
![sin(x)=((2tg((x/2)))/(1+tg^2 ((x/2)))) ⇔∫_0 ^1 ((1+tg^2 ((x/2)))/(2tg((x/2))))−(1/x)dx =∫_t ^1 (1/(tg((x/2)))).d(tg((x/2)))−∫_t ^1 (dx/x)=f(t) =ln(tg((x/2)))−ln(x)]_t ^1 =ln(tg((1/2)))+ln((t/(tg((t/2))))) lim_(x→0) f(x)=∫_0 ^1 (1/(sin(x)))−(1/x)dx lim_(x→0) f(x)=ln(tg((1/2)))+ln(2) =ln(2tg((1/2)))](Q144894.png)
$$ \\ $$$${sin}\left({x}\right)=\frac{\mathrm{2}{tg}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+{tg}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+{tg}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{tg}\left(\frac{{x}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{{x}}{dx} \\ $$$$=\int_{{t}} ^{\mathrm{1}} \frac{\mathrm{1}}{{tg}\left(\frac{{x}}{\mathrm{2}}\right)}.{d}\left({tg}\left(\frac{{x}}{\mathrm{2}}\right)\right)−\int_{{t}} ^{\mathrm{1}} \frac{{dx}}{{x}}={f}\left({t}\right) \\ $$$$\left.={ln}\left({tg}\left(\frac{{x}}{\mathrm{2}}\right)\right)−{ln}\left({x}\right)\right]_{{t}} ^{\mathrm{1}} \\ $$$$={ln}\left({tg}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{ln}\left(\frac{{t}}{{tg}\left(\frac{{t}}{\mathrm{2}}\right)}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{sin}\left({x}\right)}−\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)={ln}\left({tg}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{ln}\left(\mathrm{2}\right) \\ $$$$={ln}\left(\mathrm{2}{tg}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 30/Jun/21
$$\:\:\:\:{very}\:{nice}\:{solution}... \\ $$
Commented by qaz last updated on 30/Jun/21

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot} \\ $$
Commented by mindispower last updated on 04/Jul/21

$${pleasur}\:{sir} \\ $$
