
Question Number 205750 by MetaLahor1999 last updated on 29/Mar/24
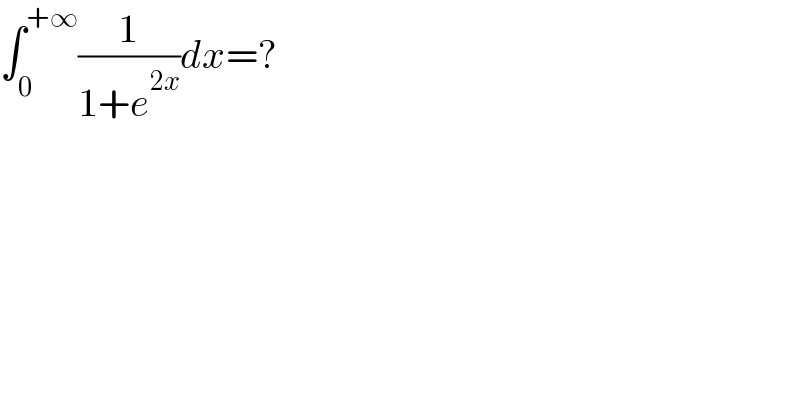
$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx}=? \\ $$
Commented by mokys last updated on 29/Mar/24
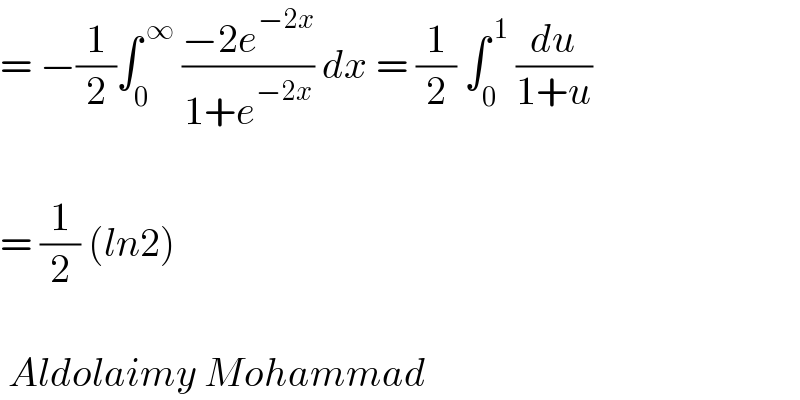
$$=\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \:\frac{−\mathrm{2}{e}^{−\mathrm{2}{x}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{du}}{\mathrm{1}+{u}} \\ $$$$ \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left({ln}\mathrm{2}\right) \\ $$$$ \\ $$$$\:{Aldolaimy}\:{Mohammad} \\ $$
Commented by MetaLahor1999 last updated on 29/Mar/24

$${thank}\:{u} \\ $$
Commented by mokys last updated on 29/Mar/24

$${welcome} \\ $$
Answered by lepuissantcedricjunior last updated on 29/Mar/24
![∫_0 ^∞ (dx/(1+e^(2x) ))=∫_0 ^∞ (e^(−2x) /(1+e^(−2x) ))dx=−(1/2)∫_0 ^∞ ((−2e^(−2x) )/(1+e^(−2x) ))dx =−(1/2)[ln(1+e^(−2x) )]_0 ^∞ =ln(√2) ∫_0 ^∞ (dx/(1+e^(2x) ))=ln((√2)) ===================== .......le puissant Dr.......................](Q205760.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{d}\boldsymbol{{x}}}{\mathrm{1}+\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} }=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} }{\mathrm{1}+\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} }\boldsymbol{{dx}}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{−\mathrm{2}\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} }{\mathrm{1}+\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} }\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{x}}} \right)\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{ln}}\sqrt{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{x}}} }=\boldsymbol{{ln}}\left(\sqrt{\mathrm{2}}\right) \\ $$$$===================== \\ $$$$.......{le}\:{puissant}\:\boldsymbol{{D}}{r}....................... \\ $$
Answered by mathzup last updated on 31/Mar/24
![I=∫_0 ^∞ (dx/(1+e^(2x) ))=_(e^x =t) ∫_1 ^∞ (dt/(t(1+t^2 ))) =∫_1 ^∞ ((1/t)−(t/(1+t^2 )))dt =[lnt−(1/2)ln(1+t^2 )]_1 ^∞ =[ln((t/( (√(1+t^2 )))))]_1 ^∞ =0−ln((1/( (√2))))=(1/2)ln(2)](Q205809.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\mathrm{1}+{e}^{\mathrm{2}{x}} }=_{{e}^{{x}} ={t}} \:\:\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{{t}}−\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\left[{lnt}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\right]_{\mathrm{1}} ^{\infty} =\left[{ln}\left(\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)\right]_{\mathrm{1}} ^{\infty} \\ $$$$=\mathrm{0}−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$
