
Question Number 95673 by Rio Michael last updated on 26/May/20
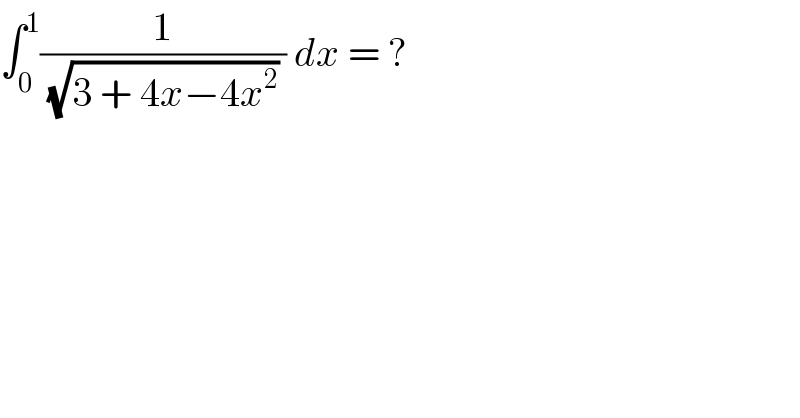
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{3}\:+\:\mathrm{4}{x}−\mathrm{4}{x}^{\mathrm{2}} }\:}\:{dx}\:=\:? \\ $$
Commented by Tony Lin last updated on 26/May/20
![∫_0 ^1 (1/(√(3+4x−4x^2 )))dx =∫_0 ^1 (1/(√(−4(x^2 −x+(1/4))+4)))dx =(1/2)∫_0 ^1 (1/(√(1−(x−(1/2))^2 )))dx =[(1/2)sin^(−1) (x−(1/2))]_0 ^1 =(π/6)](Q95678.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{3}+\mathrm{4}{x}−\mathrm{4}{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{−\mathrm{4}\left({x}^{\mathrm{2}} −{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{1}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }}{dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{6}} \\ $$
Commented by Rio Michael last updated on 26/May/20

$$\mathrm{thanks}\: \\ $$
