
Question Number 220848 by Nicholas666 last updated on 20/May/25
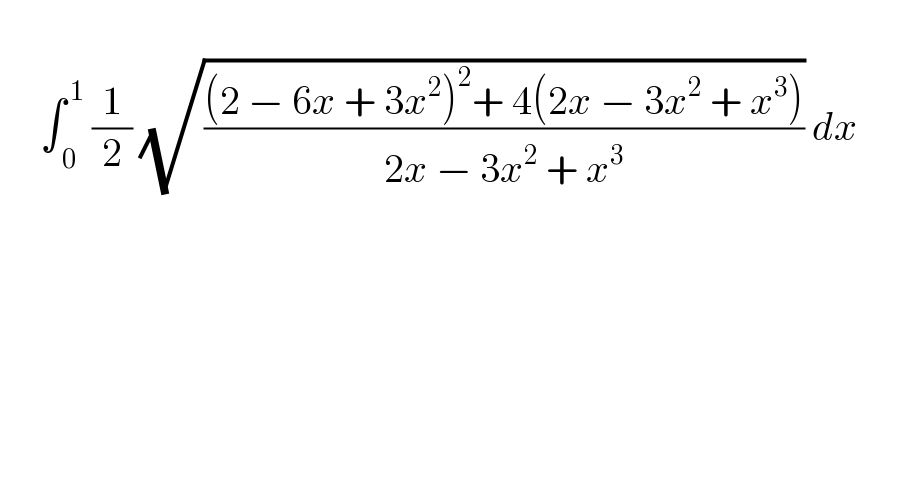
$$ \\ $$$$\:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{2}}\:\sqrt{\frac{\left(\mathrm{2}\:−\:\mathrm{6}{x}\:+\:\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\:\mathrm{4}\left(\mathrm{2}{x}\:−\:\mathrm{3}{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{3}} \right)}{\mathrm{2}{x}\:−\:\mathrm{3}{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{3}} }}\:{dx}\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by MathematicalUser2357 last updated on 20/May/25
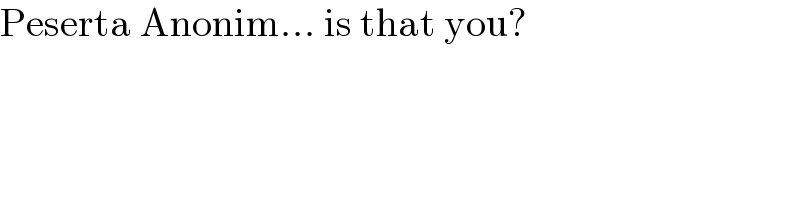
$$\mathrm{Peserta}\:\mathrm{Anonim}...\:\mathrm{is}\:\mathrm{that}\:\mathrm{you}? \\ $$
Commented by Nicholas666 last updated on 20/May/25

$${yes} \\ $$
Answered by Wuji last updated on 20/May/25
![∫^(1/2) _0 (1/2)(√(((2−6x+3x^2 )^2 +4(2x−3x^2 +x^3 ))/(2x−3x^2 +x^3 )))dx let g(x)=2x−3x^2 +x^3 ⇒g′(x)=2−6x+3x^2 Δ(x)=(√((g′(x))^2 +4g(x))) f(x) =((Δ(x))/( (√(g(x))))) +2ln(((g′(x)+Δ(x))/(2(√(g(x)))))) ⇒f′(x)=(√(((g′(x))^2 +4g(x))/(g(x)))) apply product chain rule (d/dx)[Δ(x)/(√(g(x)))]=(d/dx)[Δg^(−1/2) ]=((Δ′(√g)−Δ((g′)/(2(√g))))/g) (d/dx)[2ln(((g′+Δ)/(2(√g))))] =(d/dx)[2ln(g′+Δ)] =2((g′′+Δ′)/(g′+Δ)) Δ′(x)=((g′(x)g′′(x)+2g′(x))/(Δ(x)))=(√(((g′)^2 4g)/g)) ⇒∫_. ^(1/2) (1/2)(√(((g′)^2 +4g)/g))dx =f((1/2))−lim_(x→0) f(x) g((1/2))=2(1/2)−3((1/2))^2 +((1/2))^3 =1−(3/4)+(1/8) =(3/8) g′((1/2))=2−6((1/2))+3((1/2))^2 =2−3+(3/4) =(−(1/4))^2 =(1/(16)) Δ((1/2))=(√((1/(16))+4•(3/8)))=(√((1/(16))+(3/2)))=(√((25)/(16))) =(5/4) f((1/2))=((5/4)/( (√(3/8))))+2ln(((−2/4+5/4)/(2(√(3/8)))))=(5/4)•(2/( (√3)))+2ln((1/( (√6)/2)))=(5/(2(√3)))+2ln((2/( (√6)))) for x→0 g(x)∼2x ⇒g′(x)∼2. Δ(x)∼(√(4+8x)) ∼2+((2x)/2)=2+x ((Δ(x))/( (√(g(x))))) ∼ ((2+x)/( (√(2x)))) →^0 +∞ ⇒lim_(x→0) f(x)=2ln(2) ⇒∫_0 ^(1/2) (1/2)(√(((2−6x+3x^2 )^2 +4(2x−3x^2 +x^3 ))/((2x−3x^2 +x^3 ))))dx =(1/2)((5/(2(√3)))+2ln((2/( (√6))))−2ln(2)) 2ln((2/( (√6))))−2ln(2)=2ln((2/( (√6)))•(1/2))=−ln(6) ⇒ (1/2)((5/(2(√3)))−ln(6)) =(5/(4(√3)))−(1/2)ln(6) ⇒∫_0 ^(1/2) (1/2)(√(((2−6x+3x^2 )+4(2x−3x^2 +x^3 ))/((2x−3x^2 +x^3 ))))dx =(5/(4(√3)))−(1/2)ln(6)](Q220930.png)
$$ \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\int}^{\mathrm{1}/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(\mathrm{2}−\mathrm{6}{x}+\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)}{\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }}{dx} \\ $$$${let}\:{g}\left({x}\right)=\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \:\:\Rightarrow{g}'\left({x}\right)=\mathrm{2}−\mathrm{6}{x}+\mathrm{3}{x}^{\mathrm{2}} \\ $$$$\Delta\left({x}\right)=\sqrt{\left({g}'\left({x}\right)\right)^{\mathrm{2}} +\mathrm{4}{g}\left({x}\right)} \\ $$$${f}\left({x}\right)\:=\frac{\Delta\left({x}\right)}{\:\sqrt{{g}\left({x}\right)}}\:+\mathrm{2}{ln}\left(\frac{{g}'\left({x}\right)+\Delta\left({x}\right)}{\mathrm{2}\sqrt{{g}\left({x}\right)}}\right)\:\:\Rightarrow{f}'\left({x}\right)=\sqrt{\frac{\left({g}'\left({x}\right)\right)^{\mathrm{2}} +\mathrm{4}{g}\left({x}\right)}{{g}\left({x}\right)}} \\ $$$${apply}\:{product}\:{chain}\:{rule} \\ $$$$\frac{{d}}{{dx}}\left[\Delta\left({x}\right)/\sqrt{{g}\left({x}\right)}\right]=\frac{{d}}{{dx}}\left[\Delta{g}^{−\mathrm{1}/\mathrm{2}} \right]=\frac{\Delta'\sqrt{{g}}−\Delta\frac{{g}'}{\mathrm{2}\sqrt{{g}}}}{{g}} \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{2}{ln}\left(\frac{{g}'+\Delta}{\mathrm{2}\sqrt{{g}}}\right)\right]\:=\frac{{d}}{{dx}}\left[\mathrm{2}{ln}\left({g}'+\Delta\right)\right]\:=\mathrm{2}\frac{{g}''+\Delta'}{{g}'+\Delta} \\ $$$$\Delta'\left({x}\right)=\frac{{g}'\left({x}\right){g}''\left({x}\right)+\mathrm{2}{g}'\left({x}\right)}{\Delta\left({x}\right)}=\sqrt{\frac{\left({g}'\right)^{\mathrm{2}} \mathrm{4}{g}}{{g}}} \\ $$$$\Rightarrow\int_{.} ^{\mathrm{1}/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({g}'\right)^{\mathrm{2}} +\mathrm{4}{g}}{{g}}}{dx}\:={f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right) \\ $$$${g}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}\:=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$${g}'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}−\mathrm{6}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{2}−\mathrm{3}+\frac{\mathrm{3}}{\mathrm{4}}\:=\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\Delta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{1}}{\mathrm{16}}+\mathrm{4}\bullet\frac{\mathrm{3}}{\mathrm{8}}}=\sqrt{\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{25}}{\mathrm{16}}}\:=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{5}/\mathrm{4}}{\:\sqrt{\mathrm{3}/\mathrm{8}}}+\mathrm{2}{ln}\left(\frac{−\mathrm{2}/\mathrm{4}+\mathrm{5}/\mathrm{4}}{\mathrm{2}\sqrt{\mathrm{3}/\mathrm{8}}}\right)=\frac{\mathrm{5}}{\mathrm{4}}\bullet\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}+\mathrm{2}{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}/\mathrm{2}}\right)=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{3}}}+\mathrm{2}{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\right) \\ $$$${for}\:{x}\rightarrow\mathrm{0} \\ $$$${g}\left({x}\right)\sim\mathrm{2}{x}\:\Rightarrow{g}'\left({x}\right)\sim\mathrm{2}.\:\:\Delta\left({x}\right)\sim\sqrt{\mathrm{4}+\mathrm{8}{x}}\:\sim\mathrm{2}+\frac{\mathrm{2}{x}}{\mathrm{2}}=\mathrm{2}+{x} \\ $$$$\frac{\Delta\left({x}\right)}{\:\sqrt{{g}\left({x}\right)}}\:\sim\:\frac{\mathrm{2}+{x}}{\:\sqrt{\mathrm{2}{x}}}\:\:\overset{\mathrm{0}} {\rightarrow}\:+\infty \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{2}{ln}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(\mathrm{2}−\mathrm{6}{x}+\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)}{\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)}}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{3}}}+\mathrm{2}{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)\right) \\ $$$$\mathrm{2}{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\right)−\mathrm{2}{ln}\left(\mathrm{2}\right)=\mathrm{2}{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}}\bullet\frac{\mathrm{1}}{\mathrm{2}}\right)=−{ln}\left(\mathrm{6}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{3}}}−{ln}\left(\mathrm{6}\right)\right)\:=\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{6}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(\mathrm{2}−\mathrm{6}{x}+\mathrm{3}{x}^{\mathrm{2}} \right)+\mathrm{4}\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)}{\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{2}} +{x}^{\mathrm{3}} \right)}}{dx}\:=\frac{\mathrm{5}}{\mathrm{4}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{6}\right)\: \\ $$
