
Question Number 218150 by Shrodinger last updated on 31/Mar/25
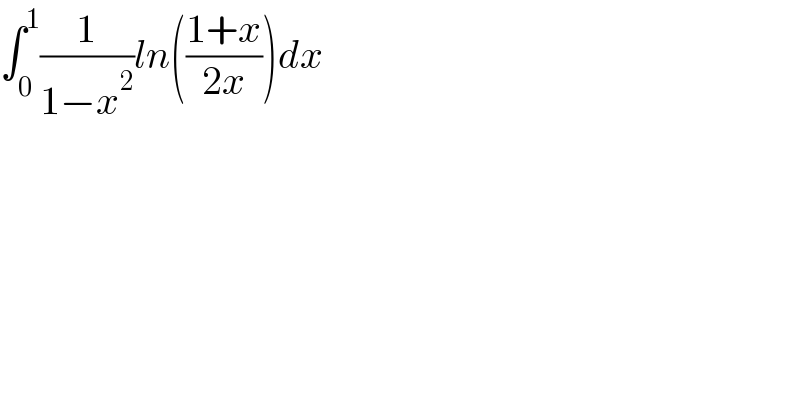
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}{x}}\right){dx} \\ $$
Answered by MrGaster last updated on 31/Mar/25
![∫_0 ^1 (1/(1−x^2 ))ln(((1+x)/(2x)))dx=∫_0 ^1 ((ln(1+x))/(1−x^2 ))dx−∫_0 ^1 ((ln(2x))/(1−x^2 ))dx ∫_0 ^1 ((ln(1+x))/(1−x^2 ))dx=∫_0 ^1 ln(1+x)((1/2)((1/(1−x))+(1/(1+x))))dx =(1/2)(∫_0 ^1 ((ln(1+x))/(1−x))dx+∫_0 ^1 ((ln(1+x))/(1+x))dx) =(1/2)(∫_0 ^1 ((ln(1+x))/(1−x))dx+[(1/2)ln^2 (1+x)]_0 ^1 ) =(1/2)(∫_0 ^1 ((ln(1+x))/(1−x))dx+(1/2)ln^2 (2)) ∫_0 ^1 ((ln(1+x))/(1−x))dx=∫_0 ^1 ln(1+x)Σ_(n=0) ^∞ x^n dx=Σ_(n=0) ^∞ ∫_0 ^1 x^n ln(1+x)dx =Σ_(n=0) ^∞ ((((−1)^(n+1) )/(n+1))−(((−1)^(n+1) )/((n+1)^2 )))=(π^2 /(12)) ∫_0 ^1 ((ln(2x))/(1−x^2 ))dx=∫_0 ^1 ((ln(2)+ln(x))/(1−x^2 ))dx=ln(2)∫_0 ^1 (1/(1−x^2 ))dx+∫_0 ^1 ((ln(x))/(1−x^2 ))dx [(1/2)ln(((1+x)/(1−x)))]_0 ^1 +[(1/2)ln^2 (x)]_0 ^1 =(π/4)ln(2) ∫_0 ^1 (1/(1−x^2 ))ln(((1+x)/(2x)))dx=(π^2 /(12))−(π^4 /4)ln(2)+(π/4)ln(2)=(π^2 /(12))](Q218152.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}{x}}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{2}{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+{x}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}+\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx}+\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+{x}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}−\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{2}{x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}=\mathrm{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}^{\mathrm{2}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\mathrm{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{2}{x}}\right){dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\pi^{\mathrm{4}} }{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
