Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 194759 by horsebrand11 last updated on 15/Jul/23

∫_0 ^( 1) ∫_0 ^( 1) (((1+x^2 )/(1+x^2 +y^2 ))) dxdy

$$\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\left(\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\right)\:\mathrm{dxdy}\: \\ $$

Commented by Frix last updated on 15/Jul/23

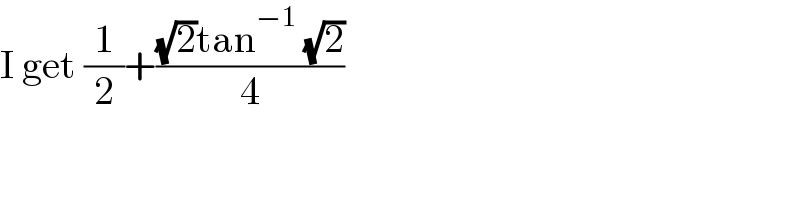
I get (1/2)+(((√2)tan^(−1) (√2))/4)

$$\mathrm{I}\:\mathrm{get}\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$

Answered by dimentri last updated on 15/Jul/23

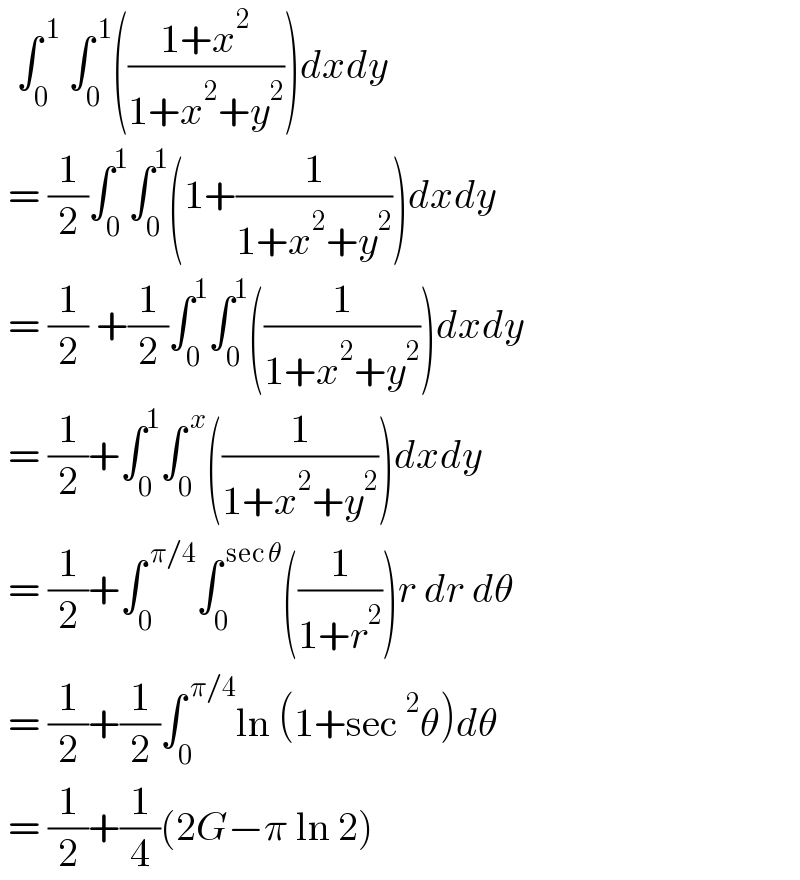
∫_0 ^( 1) ∫_0 ^( 1) (((1+x^2 )/(1+x^2 +y^2 )))dxdy = (1/2)∫_0 ^1 ∫_0 ^1 (1+(1/(1+x^2 +y^2 )))dxdy = (1/2) +(1/2)∫_0 ^1 ∫_0 ^1 ((1/(1+x^2 +y^2 )))dxdy = (1/2)+∫_0 ^1 ∫_0 ^( x) ((1/(1+x^2 +y^2 )))dxdy = (1/2)+∫_0 ^( π/4) ∫_0 ^( sec θ) ((1/(1+r^2 )))r dr dθ = (1/2)+(1/2)∫_0 ^( π/4) ln (1+sec^2 θ)dθ = (1/2)+(1/4)(2G−π ln 2)

$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){dxdy}\: \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){dxdy} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){dxdy} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\:{x}} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right){dxdy}\: \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \int_{\mathrm{0}} ^{\:\mathrm{sec}\:\theta} \left(\frac{\mathrm{1}}{\mathrm{1}+{r}^{\mathrm{2}} }\right){r}\:{dr}\:{d}\theta \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\pi/\mathrm{4}} \mathrm{ln}\:\left(\mathrm{1}+\mathrm{sec}\:^{\mathrm{2}} \theta\right){d}\theta \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{G}−\pi\:\mathrm{ln}\:\mathrm{2}\right)\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com