
Question Number 26949 by Joel578 last updated on 31/Dec/17
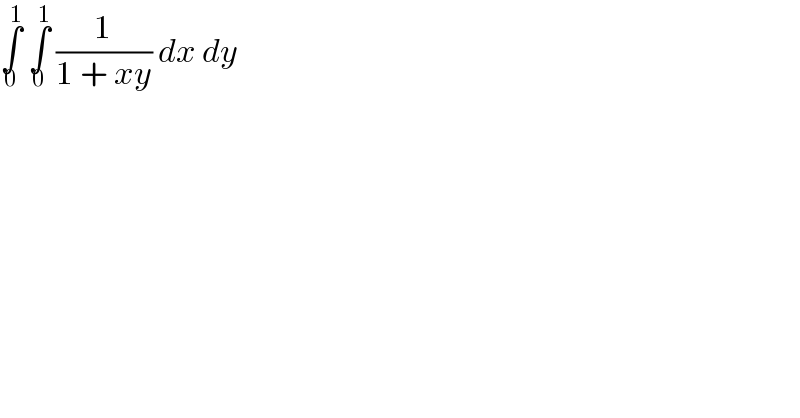
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{1}}{\mathrm{1}\:+\:{xy}}\:{dx}\:{dy} \\ $$
Commented by abdo imad last updated on 31/Dec/17
![I= ∫_0^ ^1 ( ∫_0 ^1 (dx/(1+xy)))dy=∫_0 ^1 ((1/y)ln(1+xy)]_(x=0) ^(x=1) )dy = ∫_0 ^1 ((ln(1+y))/y)dy but ∂ln(1+y)/∂y= (1/(1+y)) = Σ_(n=0) ^∝ (−1)^n y^n with /y/<1 and ln(1+y) = Σ _(n=0)^∝ (((−1)^n )/(n+1)) y^(n+1) = Σ_(n=1) ^∝ (((−1)^(n−1) )/n) y^n ⇒ ∫_0 ^1 ((ln(1+y))/y)dy = ?∫_0 ^1 (Σ_(n=1) ^∝ (((−1)^(n−1) )/n) y^(n−1) ) = Σ_(n=1) ^∝ (((−1)^(n−1) )/n^2 ) but Σ_(n=1) ^∝ (((−1)^(n−1) )/n^2 ) = −Σ_(n=1) ^α (1/(4n^2 )) +Σ_(n=0) ^∝ (1/((2n+1)^2 )) = −(1/4) (π^2 /6)+ (π^2 /8) = (π^2 /(12)).](Q26960.png)
$$\left.{I}=\:\int_{\mathrm{0}^{} } ^{\mathrm{1}} \left(\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{xy}}\right){dy}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{y}}{ln}\left(\mathrm{1}+{xy}\right)\right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \right){dy} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{y}\right)}{{y}}{dy}\:\:\:\:{but}\:\:\partial{ln}\left(\mathrm{1}+{y}\right)/\partial{y}=\:\frac{\mathrm{1}}{\mathrm{1}+{y}}\:=\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\left(−\mathrm{1}\right)^{{n}} {y}^{{n}} \:\:\:\:{with}\:/{y}/<\mathrm{1} \\ $$$${and}\:\:{ln}\left(\mathrm{1}+{y}\right)\:=\:\Sigma\:_{{n}=\mathrm{0}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{y}^{{n}+\mathrm{1}} \:=\:\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{y}^{{n}} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{y}\right)}{{y}}{dy}\:=\:?\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{y}^{{n}−\mathrm{1}} \:\right) \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\:{but}\:\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\propto} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }\:=\:−\sum_{{n}=\mathrm{1}} ^{\alpha} \:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\propto} \frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\:\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}}. \\ $$
Commented by Joel578 last updated on 01/Jan/18
$${thank}\:{you}\:{very}\:{much} \\ $$
