
Question Number 173069 by mnjuly1970 last updated on 06/Jul/22
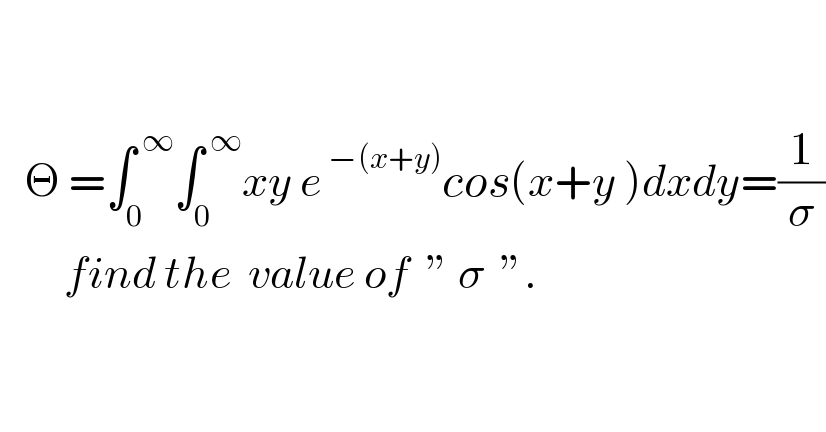
$$ \\ $$$$ \\ $$$$\:\:\:\Theta\:=\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {xy}\:{e}^{\:−\left({x}+{y}\right)} {cos}\left({x}+{y}\:\right){dxdy}=\frac{\mathrm{1}}{\sigma} \\ $$$$\:\:\:\:\:\:\:\:{find}\:{the}\:\:{value}\:{of}\:\:''\:\sigma\:\:''. \\ $$$$ \\ $$
Answered by aleks041103 last updated on 07/Jul/22
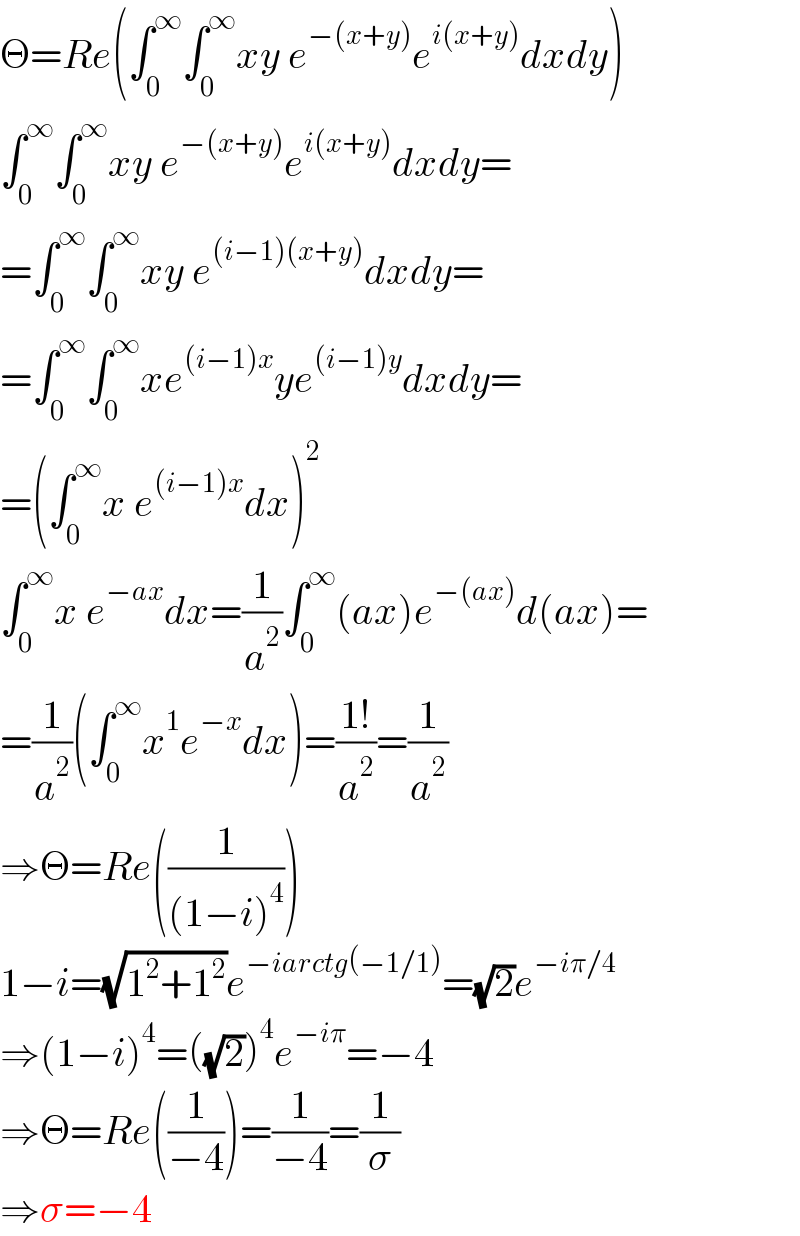
$$\Theta={Re}\left(\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {xy}\:{e}^{−\left({x}+{y}\right)} {e}^{{i}\left({x}+{y}\right)} {dxdy}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {xy}\:{e}^{−\left({x}+{y}\right)} {e}^{{i}\left({x}+{y}\right)} {dxdy}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {xy}\:{e}^{\left({i}−\mathrm{1}\right)\left({x}+{y}\right)} {dxdy}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {xe}^{\left({i}−\mathrm{1}\right){x}} {ye}^{\left({i}−\mathrm{1}\right){y}} {dxdy}= \\ $$$$=\left(\int_{\mathrm{0}} ^{\infty} {x}\:{e}^{\left({i}−\mathrm{1}\right){x}} {dx}\right)^{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}\:{e}^{−{ax}} {dx}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \left({ax}\right){e}^{−\left({ax}\right)} {d}\left({ax}\right)= \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left(\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}} {e}^{−{x}} {dx}\right)=\frac{\mathrm{1}!}{{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{{a}^{\mathrm{2}} } \\ $$$$\Rightarrow\Theta={Re}\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{i}\right)^{\mathrm{4}} }\right) \\ $$$$\mathrm{1}−{i}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }{e}^{−{iarctg}\left(−\mathrm{1}/\mathrm{1}\right)} =\sqrt{\mathrm{2}}{e}^{−{i}\pi/\mathrm{4}} \\ $$$$\Rightarrow\left(\mathrm{1}−{i}\right)^{\mathrm{4}} =\left(\sqrt{\mathrm{2}}\right)^{\mathrm{4}} {e}^{−{i}\pi} =−\mathrm{4} \\ $$$$\Rightarrow\Theta={Re}\left(\frac{\mathrm{1}}{−\mathrm{4}}\right)=\frac{\mathrm{1}}{−\mathrm{4}}=\frac{\mathrm{1}}{\sigma} \\ $$$$\Rightarrow\sigma=−\mathrm{4} \\ $$
Commented by aleks041103 last updated on 07/Jul/22
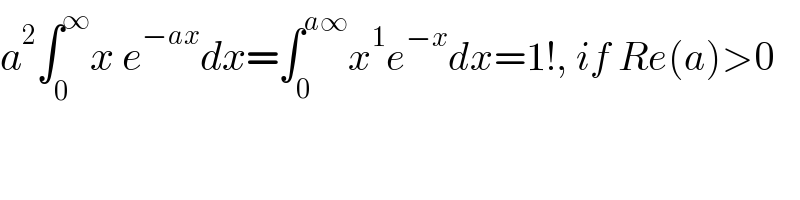
$${a}^{\mathrm{2}} \int_{\mathrm{0}} ^{\infty} {x}\:{e}^{−{ax}} {dx}=\int_{\mathrm{0}} ^{{a}\infty} {x}^{\mathrm{1}} {e}^{−{x}} {dx}=\mathrm{1}!,\:{if}\:{Re}\left({a}\right)>\mathrm{0} \\ $$
Answered by Eulerian last updated on 07/Jul/22
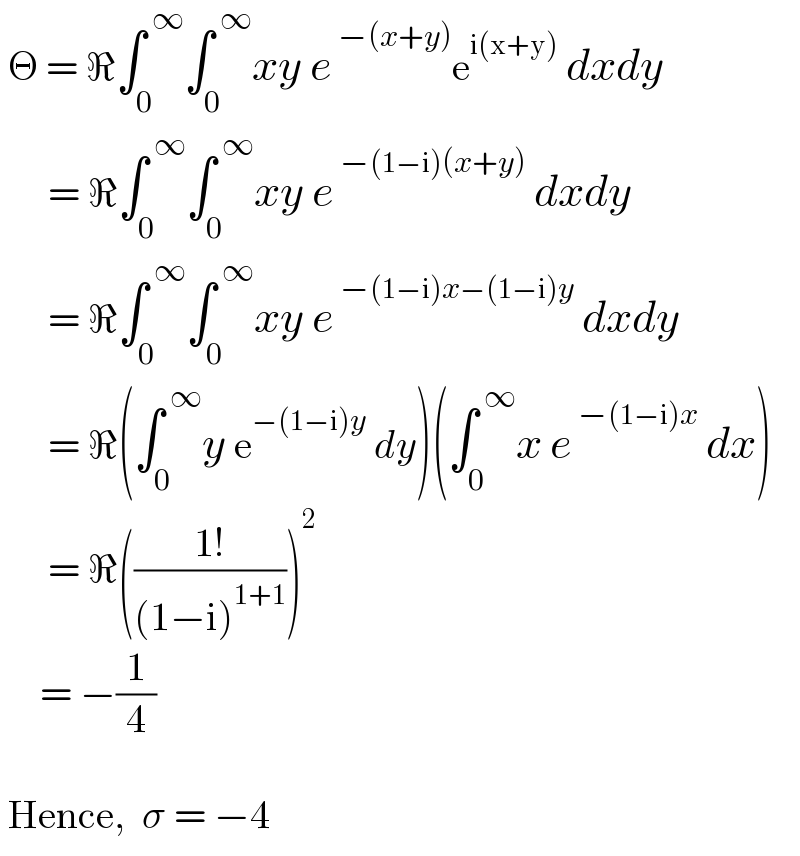
$$\:\Theta\:=\:\Re\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {xy}\:{e}^{\:−\left({x}+{y}\right)} \mathrm{e}^{\mathrm{i}\left(\mathrm{x}+\mathrm{y}\right)} \:{dxdy} \\ $$$$\:\:\:\:\:\:=\:\Re\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {xy}\:{e}^{\:−\left(\mathrm{1}−\mathrm{i}\right)\left({x}+{y}\right)} \:{dxdy} \\ $$$$\:\:\:\:\:\:=\:\Re\int_{\mathrm{0}} ^{\:\infty} \int_{\mathrm{0}} ^{\:\infty} {xy}\:{e}^{\:−\left(\mathrm{1}−\mathrm{i}\right){x}−\left(\mathrm{1}−\mathrm{i}\right){y}} \:{dxdy} \\ $$$$\:\:\:\:\:\:=\:\Re\left(\int_{\mathrm{0}} ^{\:\infty} {y}\:\mathrm{e}^{−\left(\mathrm{1}−\mathrm{i}\right){y}} \:{dy}\right)\left(\int_{\mathrm{0}} ^{\:\infty} {x}\:{e}^{\:−\left(\mathrm{1}−\mathrm{i}\right){x}} \:{dx}\right) \\ $$$$\:\:\:\:\:\:=\:\Re\left(\frac{\mathrm{1}!}{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{1}+\mathrm{1}} }\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\: \\ $$$$\:\mathrm{Hence},\:\:\sigma\:=\:−\mathrm{4} \\ $$
